Табулирование функций.

Задача табулирования функции предполагает получение таблицы значений функции при изменении аргумента с фиксированным шагом. В качестве исходной информации должны быть заданы: Х₀, Х_n – начало и конец промежутка табулирования, при этом (Х0< Х_n); n – число шагов разбиения промежутка [Х₀, X_n]; F(X) – описание табулируемой функции.

При составлении алгоритма предполагается, что X – текущее значение аргумента; h – шаг изменения аргумента (иногда его называют шагом табуляции функции); i – текущий номер точки, в которой вычисляются функция (i = 0 .. n).
Количество интервалов n, шаг табуляции h и величины Х₀, Х_n связаны между собой фор-мулой:

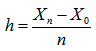
Интерпретация переменных (т. е. их обозначение в математической постановке задачи, смысл и тип, обозначения в блок-схеме и программе) приведена в таблице имен.

Пример 17. Табулировать функцию F(X) в N равноотстоящих точках, заданную на промежутке [Х₀, X_n], где

PROGRAM PR17;
VAR
I, N: INTEGER;
X, Y: REAL;
H, X0, XN: REAL;
BEGIN
WRITELN('ВВЕДИТЕ X0, XN, N');
READLN(X0, XN, N);
H := (XN - X0)/N;
FOR I:=0 TO N
DO BEGIN
       Y:= SIN(X+1)*EXP(2-X*X);
       X := X0 + I * H;
       WRITELN (X:4:1,",Y:9:6)
       END
END.

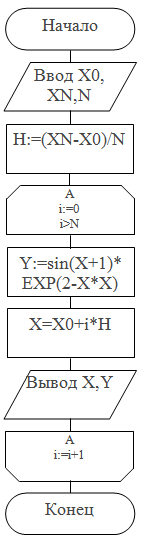
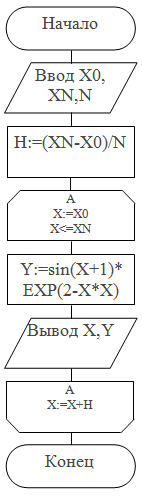
Теперь запишем решение этой же задачи, но с использованием цикла While...DO.

PROGRAM PR17_while;
VAR
N: INTEGER;
X, Y: REAL;
H, X0, XN: REAL;
BEGIN
WRITELN('ВВЕДИТЕ X0, XN, N');
READLN(X0, XN, N);
H := (XN - X0)/N;
X:=X0;
WHILE X<=XN
DO BEGIN
       Y:= SIN(X+1)*EXP(2-X*X);
       X := X + H;
       WRITELN (X:4:1,",Y:9:6)
       END
END.

Предыдущая статья: Примеры использования различных операторов цикла.
Оглавление: Лекции по Pascal.
Следующая статья: Арифметический цикл с рекуррентной зависимостью.