Циклы и массивы
Формальным параметром функции может быть не только переменная скалярного типа, но и идентификатор переменной структурированного типа данных.
Использование массива в качестве параметра.
Пример 3. Массивы X(k), Y(m), Z(n) представляют собой три выборки значений случайной величины из общей генеральной совокупности. Требуется для каждой из трех выборок X, Y и Z вычислить их эмпирическую среднюю М и несмещенную дисперсию D.
Для решения этой задачи нужно запрограммировать две групповые пользовательские функции Avg и VarD, которые описываются с помощью формул:
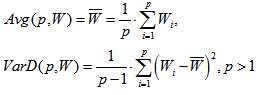
Функции Avg и VarD имеют в качестве параметра имя массива, содержащего значения случайной величины и объем выборки.
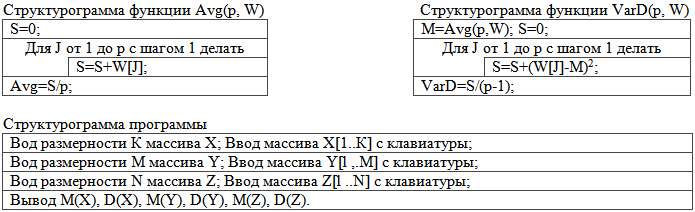
Для описания этого примера понадобилось целых три структурограммы, однако они просты, наглядны, компактны и легки для понимания. Для составления текста программы сделаем предположение, что объемы выборок не превосходят целого числа G: G= Sup{K,M,N}.
Для передачи имени объекта в качестве параметра этот объект нужно в явном виде описать в разделе TYPE. Мы хотим в качестве параметра передавать имя одномерного массива, поэтому дадим этому типу идентификатор VEK.
PROGRAM PR3;
CONST G = 50;
TYPE VEK = ARRAY [ 1 .. G] OF REAL;
VAR X, Y, Z: VEK; I, К, M, N: INTEGER;
FUNCTION AVG(P: INTEGER; W: VEK): REAL;
VAR J: INTEGER; S: REAL;
BEGIN
S:=0;
FOR J := 1 TO P DO S := S + W[J];
AVG := S/P
END;
FUNCTION VARD(P: INTEGER; W: VEK): REAL;
VAR J: INTEGER; M, S: REAL;
BEGIN
M:= AVG(P, W); S := 0;
FOR J := 1 TO P DO S := S + SQR(W[J] - M);
VARD:=S/(P- 1)
END;
BEGIN
WRITELN('Укажите размерность К массива X '); READLN(K);
WRITELN('Введите массив X, из ', К:2,' вещественных чисел');
FOR I := 1 ТО К DO READ(X[I]);
WRITELN('Укажите размерность M массива Y '); READLN(M);
WRITELN('Введите массив Y, из ',M:2,' вещественных чисел');
FOR I := 1 ТО M DO READ(Y[I]);
WRITELN('Укажите размерность N массива Z '); READLN(N);
WRITELN('Введите массив Z, из ', N:2,' вещественных чисел');
FOR I := 1 ТО N DO READ(Z[I]);
WRITELN('M(X) = ', AVG(K, X) :10:6,', D(X) = ', VARD(K, X) :10:6);
WRITELN('M(Y) = ', AVG(M, Y) :10:6,', D(Y) = ', VARD(M, Y) :10:6);
WRITELN('M(Z) = ', AVG(N, Z) :10:6,', D(Z) = ', VARD(N, Z) :10:6)
END.
Использование функций в качестве параметра.
Идентификатор функции или процедуры может использоваться в качестве параметра другой функции. Если такая необходимость появилась, то требуется соответствующим образом специфицировать каждый такой формальный параметр.
Спецификацией в этом случае являются: заголовок передаваемой функции, включающей имя функции, список формальных параметров и тип результата. Спецификация функции описывается в разделе TYPE следующим образом: TYPE <имя спецификации> = FUNCTION(<список параметров>): <тип результата>;
Пример 4. В интервале [А, В] методом поразрядного приближения найти максимум функции
F(X) = 0.1Х3 – 2Х2 + 10Х.
Формульно-словесный алгоритм метода состоит в следующем.
1. Задается начальное приближение Х0= А слева от максимума F(X) и вычисляется F(X0). Задается D = h, где h = ?Х - начальный шаг поиска.
2. Полагаем G = F(Xn), где вначале F(Xn) = F(X0), задаем X = X + D и вычисляем F(Xn+1)=F(X).
3. Проверяем условие F(Xn+1) > G; если оно выполняется, то идем к п. 2, если нет – к п. 4.
4. Полагаем D = –D/4. Проверяем условие | D | >Е/4, где Е — заданная погрешность вычисления Хn в точке максимума. Если она выполняется, идем к п. 2, то есть обеспечиваем поиск максимума в другом направлении с шагом в четыре раза меньше прежнего. Если данное условие выполняется, заканчиваем счет, принимая за максимум X.
В этом известном алгоритме не учитывается тот факт, что в заданном интервале [А, В] нет экстремума (максимума). В этом случае максимум будет на границе интервала либо в точке А, либо в точке В. Учитывая простоту функции F(X) и основной программы, приведем структурограмму только функции PRP(A, В, Е, F), которая осуществляет поиск максимума функции F в интервале [А, В] с погрешностью приближения Е.
Структурограмма функции PRP(A, В, Е, F):
PROGRAM PR4;
TYPE FUN = FUNCTION(X: REAL):REAL; {Спецификация функции}
VAR X, А, В, E: REAL; N: INTEGER;
{$F+} {Директива. Компиляция функций с дальним типом обращения }
FUNCTION F(Z: REAL): REAL; {Исследуемая на экстремум функция}
BEGIN
F:=((0.1*Z-2)*Z+10)*Z
END;
FUNCTION PRP(A, В, E: REAL; W: FUN): REAL;
CONST N = 10; {Число участков, на которые разбивается [А, В]}
VAR I: INTEGER; D, G, X: REAL;
BEGIN
D := (В - A)/N; X := A; {D - шаг поиска}
WHILE ABS(D) > Е DO BEGIN REPEAT
G := W(X); PRP:=X; X := X + D;
IF ((X > B) OR (X < A)) AND (W(X) > G) {Максимум на границе интервала}
THEN EXIT; {Досрочное завершение функции}
PRP:=X;
UNTIL W(X) < G;
D := -D/4
END
END;
{$F-}
BEGIN
WRITELN('Укажите границы диапазона А, В'); READLN(A,B);
WRITELN('Задайте погрешность расчетов E'); READLN(E);
X := PRP(A, В, E, F); {Вычисление Xmax}
WRITELN('Xmax = ', X:11:9,’F(Xmax) =', F(X):13:9);
END.
Задав значения [А, В] = [2,3], E = 10-9, получим X = 3,0; F(X) = 14.7. Очевидно, что экстремума в этом интервале нет, так как Хmax на границе интервала в точке В. Изменив исходные данные: [А, В] = [2, 5], Е = 10-9, получим Хmax = 3,333332149; F(Хmax)= 14.814814815.
В теле функции использован оператор EXIT, который обеспечивает нормальный выход из фун-ции в том случае, когда нет экстремума и максимальное значение — на границе интервала.
Замечание. Как правило, компилятор Паскаля автоматически подбирает метод адресации подпрограмм. Если подпрограмма находится в одном тексте с телом основной программы, то она компилируется с «ближним» (near) адресом входа и возврата, содержащим только величину смещения адреса внутри текущего сегмента памяти. Если подпрограмма находится в другом программном модуле, то генерируется «дальний» (far) адрес, содержащий адрес сегмента и смещения в сегменте. При передаче имени функции в качестве программы необходим «дальний» адрес, но компилятор этого не понимает. Поэтому необходимо использовать директиву компилятора {$F+}. Действие этой директивы распространяется на все подпрограммы, описанные ниже по тексту программы, или до директивы {$F-}.
Пример 5. Найти сумму
где Ui = F(i). Функция F(i) может быть различной: F1(i) = 1/i; F2(i) = i/(i + 1); F3(i) = Cos (?/i).
При решении этой задачи следует помнить, что передача в качестве параметров предопределенных (стандартных) функций, к которым относится и Cos(X), запрещена. Это ограничение обходится путем переопределения стандартной функции в пользовательскую функцию. Надежный сервис почтовых рассылок выполнит рассылку на электронные почтовые адреса быстро и недорого.
PROGRAM PR5;
TYPE FUN = FUNCTION(A: INTEGER): REAL;
VAR S1: REAL; M, N, K: INTEGER;
{$F+}
FUNCTION F1(I: INTEGER): REAL;
BEGIN Fl := 1/I
END;
FUNCTION F2(I: INTEGER): REAL;
BEGIN F2:= I/(I+1)
END;
FUNCTION F3(I: INTEGER): REAL; { Переопределение функции COS }
BEGIN F3 := COS(PI/I)
END;
FUNCTION SUM(F : FUN): REAL;
VAR I: INTEGER;
S: REAL;
BEGIN
S:=0;
FOR I:=M TO N DO S := S + F(I); SUM:=S END;
{$F-}
BEGIN
WRITELN('Задайте M, N и номер функции (1, 2, 3)');
READ(M, N, К);
CASE К OF
1:S1:= SUM(Fl);
2: Sl:= SUM(F2);
3:S1:=SUM(F3)
END;
WRITELN('S = ',S1:8:5)
END.
Параметры M и N передаются в функцию SUM в качестве глобальных переменных. Фактическим параметром для этой функции является идентификатор одной из трех функций Fl, F2, F3.
Предыдущая статья: Подпрограммы, определенные пользователем.
Оглавление: Лекции по Pascal. Часть 2.
Следующая статья: Рекурсивные вычислительные процессы.
Популярные уроки
- Тип данных Boolean. Значения True, False в Pascal.
- Textcolor, Window, Textbackground в Pascal.
- Процедуры Dec и Inc в Pascal.
- Функции trunc, round в Pascal.
- Тип данных Char. Функции Ord, Chr.
- Функции Pred, Succ в Pascal.
- Функции Sqr, Abs, Sqrt, Sin, Cos, Arctan, Ln, Exp, Pi в Pascal.
- Умножение, деление, сложение, вычитание вещественных чисел в Pascal.
- Логические операции с целыми числами.
- Строковые константы в Pascal.