Арифметический цикл с рекуррентной зависимостью.

Многие циклические вычислительные процессы используют рекуррентные зависимости при решении различных математических задач.

В общем виде формулу для рекуррентных вычислений можно представить так:

В этой рекуррентной формуле для вычисления i-го члена последовательности Y_i, где i > k, используются k предыдущих членов последовательности Y_i-1,Y_i-2,...,Y_i-k . Для вычислений по этой формуле нужно задать k первых членов последовательности – Y₀,Y₁,...,Y_k-1 .
Использование рекуррентных формул, как правило, сокращает текст программы и время ее выполнения на компьютере. Однако в большинстве случаев рекуррентную формулу нужно написать программисту, что в ряде случаев вызывает определенные трудности.

Пример 18. Вычислить значение tgx:

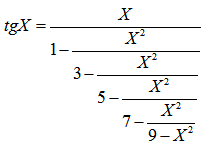
Знаменатель формулы для вычисления tgX представляет собой цепную дробь. Для вычисления такого знаменателя в цикле удобно использовать рекуррентную зависимость с памятью в один член последовательности А_i= F(A_i-1). Для вывода рекуррентной формулы следует использовать таблицу 18.

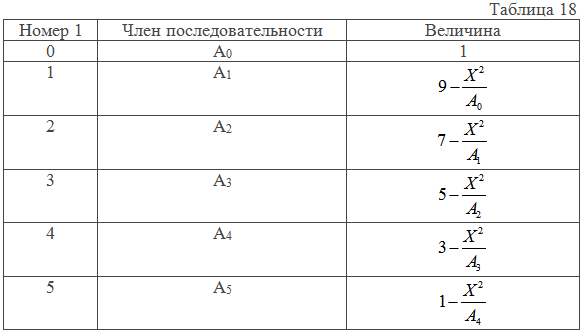
Из таблицы 23 видно, что рекуррентная формула принимает вид:

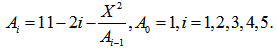
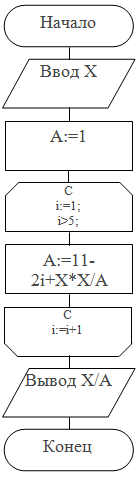
PROGRAM PR18;
VAR      
X, A: REAL;
I: INTEGER;
BEGIN
   WRITELN('BBEДИTE X');
   READLN(X);
   A := 1;
   FOR I := 1 TO 5
   DO A := 11 - 2 * I - X * X/A;
   WRITELN('tgX = ', X/A:8:5)
END.

Пример 19. Пользуясь рекуррентной формулой, для заданного N вычислить

известны Y₀, Y₁, Y₂, a Y_i(i?3) вычисляется по формуле:

Первым шагом в работе алгоритма является ввод данных Y₀, Y₁, Y₂, N. При вводе трех первых значений последовательности нужно использовать рабочие ячейки Y3, Y2 и Y1 соответственно. На втором шаге требуется проанализировать значение N. Если N < 3, то рекуррентная формула для подсчета S суммы первых N членов не потребуется. Для определения S при условии N < 3 в алгоритме предусмотрен переключатель (оператор CASE), имеющий три ветви: N = 0, N = 1 и «В противном случае», куда попадает и случай N = 2. Для каждой ветви подсчитывается соответствующая сумма S. Третий шаг выполняется только в том случае, если N > 2. На этом шаге для I от 3 до N по рекуррентной формуле вычисляются Y, и подсчитывается их сумма S. Вы можете скачать архиватор бесплатно бесплатно и без регистрации. Найденное значение S на последнем четвертом шаге выводится на экран.
PROGRAM PR19;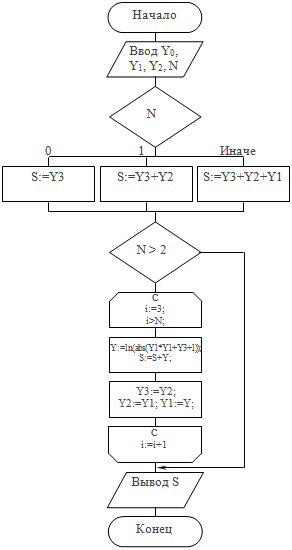
VAR     
Y3, Y2, Yl, Y, S: REAL;
I, N: INTEGER;
BEGIN
WRITELN('ВВЕДИТЕ Y0, Yl, Y2, N');
READLN(Y3, Y2, Yl, N);
CASE N OF
   0: S := Y3;
   1: S := Y3 +Y2
   ELSE S := Y3 + Y2 + Y1
END;  {CASE}
IF N > 2
THEN FOR I := 3 TO N
DO BEGIN
       Y := LN(ABS(Y1*Y1 + Y3 + 1));
       S := S + Y;
       Y3 := Y2;
       Y2 := Y1;
       Y1 := Y
       END;
WRITELN('S=', S:10:8)
END.

Предыдущая статья: Табулирование функций.
Оглавление: Лекции по Pascal.
Следующая статья: Вложенный арифметический цикл.