Организация условного перехода. Оператор IF.

Для программирования разветвляющихся процессов, содержащих две ветви, используется оператор IF условного перехода (ветвления), имеющий две конструкции.

Сокращенная форма (Алгоритм: блок-схема – рисунок 3.а, структурограмма – рисунок 4.а):
IF < Условие >
THEN < Оператор >;
В качестве условия можно использовать переменную или выражение логического типа. В этой конструкции оператор выполняется в том случае, когда логическое выражение принимает значение TRUE. Вторая ветвь процесса, содержащая пустой оператор и в явном виде не описываемая, соответствует значению условия FALSE.
Другая, полная форма этого оператора имеет синтаксическую структуру (Алгоритм: блок-схема – рисунок 3.б, структурограмма – рисунок 4.б):
IF < Условие >
THEN < Оператор 1>
ELSE < Оператор 2>;
Здесь обе ветви процесса значимы. При значении логического выражения (переменной) TRUE выполняется Оператор 1, который всегда располагается за ключевым словом THEN, при FALSE – выполняется Оператор 2 (ветвь ELSE). Если в одну из ветвей требуется включить более одного оператора, то их следует объединить составным оператором BEGIN... END.

Вложенная конструкция операторов условного перехода используется в случае, если существует более двух ветвей в вычислительном процессе. В случае вложенной конструкции Оператор 1, или Оператор 2, или оба вместе представляют собой также операторы условного перехода. В этих случаях легко запутаться при отладке программы. Но следует помнить, что ELSE всегда относится к ближайшему слева THEN.
Пример 9. Для заданного с клавиатуры значения X вычислить Y по формуле:

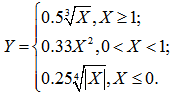
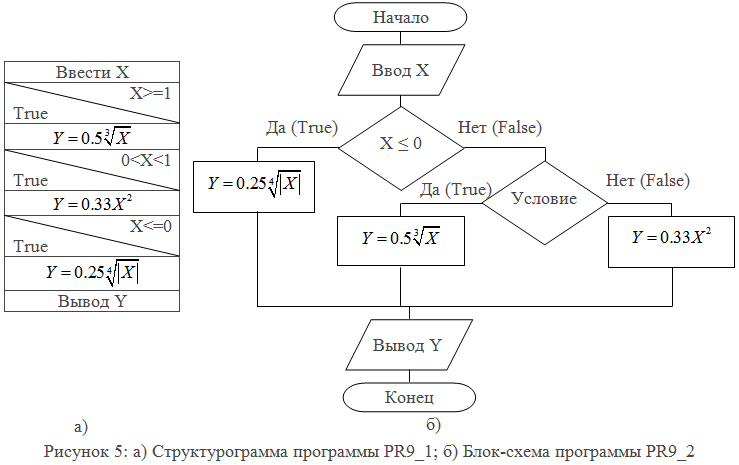
Эту задачу можно решить двумя способами. Первый способ предусматривает использование трех операторов IF сокращенной формы. Алгоритм решения достаточно прост (структурограмма на рисунке 5.а). Последовательно проверяется три взаимно исключающих друг друга условия, образующих полную группу событий. Для любого X только одно условие примет значение TRUE, остальные два условия равны FALSE. Таким образом, оператор присвоения выполнится только один раз и этот оператор будет соответствовать условию, имеющему значение TRUE. Программная реализация — PR9_1.
Второй способ предусматривает использование двух вложенных операторов IF полной формы. Алгоритм этого способа реализован в виде блок-схемы на рисунке 5.б. Программная реализация — PR9_2.
Сравнительный анализ этих двух способов показывает, что первый проще в понимании и легче в отладке. Второй способ более сложный, однако более компактный и более быстрый.
Конечно, при одной реализации вычислительного процесса это преимущество не столь существенно, но если таких реализаций десятки тысяч, то несколько секунд можно сэкономить.

PROGRAM PR9_1;
VAR X, Y: REAL;
BEGIN
WRITELN('ВВЕДИТЕ X');
READLN(X);
IF X>= 1
THEN Y:= EXP(LN(X)/3)/2;
IF (X>0) AND (X<1)
THEN Y:= X*X*0.33;
IF X<=0
THEN Y:= EXP(LN(ABS(X))/4)/4;
WRITELN('Y=',Y:10:6)
END.

---

PROGRAM PR9_2;
VAR X, Y: REAL;
BEGIN
WRITELN('ВВЕДИТЕ X');
READLN(X);
IF X<=0
THEN Y:= EXP(LN(ABS(X))/4)/4
ELSE IF X>= 1
THEN Y:= EXP(LN(X)/3)/2
ETSE Y:=X*X*0.33;
WRITELN('Y=', Y)
END.

---

Пример 10. Составить программу, которая по введенному значению X вычисляет и выводит значение Y- F(X), где F(X) задана графически на рисунке 6.

Эта задача отличается от задачи, описанной в предыдущем примере, только тем, что нужно самому составить формулу для функции F(X). В предыдущей задаче эта формула была задана в качестве исходных данных. Таким образом, от вас требуют сделать формальную, математическую постановку задачи, которая в данном случае сводится к составлению по графику формулы.
Глядя на график, нетрудно увидеть, что на нем изображена кусочно-линейная функция, содержащая три прямых линии. Первая прямая имеет уравнение Y=-X-1 и определена для X < 0. Вторая линия определена на отрезке 0 < X < 1 и имеет уравнение Y = X - 1. Третья прямая линия имеет уравнение Y = 0 и определена для X > 1. С учетом вышесказанного искомая формула будет иметь вид:

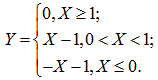
Текст программы составим по аналогии с программой PR9_2, которая подробно описана в предыдущем примере.
PROGRAM PR10;
VAR X,Y: REAL;
BEGIN
WRITELN('BBEДИTE X'); READLN(X);
IF X<=0 THEN Y:= -X-l
ELSE IF X >=1 THEN Y:= 0
ELSE Y:=X- 1;
WRITELN(Y=', Y)
END.

---

Пример 11. Найти расстояние от внешней, произвольной точки М с координатами (X, Y) до контура геометрической фигуры, изображенной на рисунке 7.

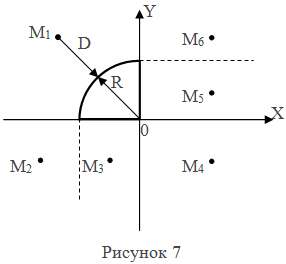
В этом задании нужно рассмотреть чертеж геометрической фигуры. Нетрудно заметить, что во втором квадранте декартовой системе координат изображен сектор круга, центр которого расположен в центре системы координат. Радиус сектора равен R. Для решения поставленной задачи требуется выделить области и для каждой из них написать уравнение, с помощью которого можно вычислить расстояние D до контура фигуры. На чертеже выделено шесть областей, в каждой из которых поставлена одна произвольная точка Мк. Номер точки К соответствует номеру области. Любая точка в области М1, имеет кратчайшее расстояние до дуги сектора, вычисляемое по формуле:

Вторая область, помеченная точкой М2, имеет кратчайшее расстояние до точки с коорди-натами (-R, 0). Это расстояние можно найти по формуле:

Третья область, помеченная точкой М3, имеет кратчайшее расстояние равное расстоянию до оси абсцисс. Это расстояние легко найти по формуле:

Четвертая область, которой соответствует точка M4, имеет кратчайшее расстояние равное расстоянию до начала координат. Это расстояние находится по формуле:

Пятая область, помеченная точкой М5, имеет кратчайшее расстояние равное расстоянию до оси ординат. Это расстояние легко найти по формуле:

Последняя шестая область, помеченная точкой М6, имеет кратчайшее расстояние до верхней точки сектора с координатами (0, R). Это расстояние можно найти по формуле:

На основании вышесказанного, математическая постановка задачи будет такой. Если точка находится вне сектора, изображенного на рисунке 7, то будет ложно условие:

Учитывая приведенные выше формулы, можно найти кратчайшее расстояние до контура фигуры по формуле:

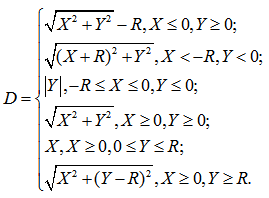
Теперь, когда формальная постановка задачи сделана и найдены формулы, можно перейти к этапу алгоритмизации (Самостоятельно) и написания программы:
PROGRAM PR11;
VAR
X, Y, R, D: REAL;
BEGIN
WRITELN('BBEДИТЕ РАДИУС СЕКТОРА R');
READLN(R);
WRITELN('BBEДИТЕ КООРДИНАТЫ ТОЧКИ X, Y');
READLN(X, Y);
IF (X<0) AND (Y>0) AND (SQRT(X*X + Y*Y)<R)
THEN WRITELN('ТОЧКА РАСПОЛОЖЕНА ВНУТРИ СЕКТОРА')
ELSE
BEGIN
IF (X<=0) AND (Y>=0)
THEN D:= SQRT(X*X + Y*Y)-R;
IF (X<=-R) AND (Y<0)
THEN D:= SQRT(SQR(X + R)+Y*Y);
IF (X<=0) AND (X>=-R) AND (Y<=0)
THEN D:= ABS(Y);
IF (X>=0) AND (Y<=0)
THEN D:= SQRT(X*X + Y*Y);
IF (X>=0) AND (Y<=R) AND (Y>=0)
THEN D:= X;
IF (X>=0) AND (Y>=R)
THEN D:= SQRT(X*X + SQR(Y-R))
END;
WRITELN('PACCTOMHHE ДО КОНТУРА СЕКТОРА D=', D:5:2)
END.

---

Предыдущая статья: Разветвляющийся вычислительный процесс.
Оглавление: Лекции по Pascal.
Следующая статья: Оператор варианта CASE.

---