Циклы и массивы
Функция может вызывать другую функцию, та в свою очередь третью и т.д. В результате программы приобретают иерархическую структуру.
Простая рекурсия.
В Паскале допускается, чтобы функция вызывала саму себя. Такой способ вызова называется простой рекурсией. Классическим примером использования рекурсии является вычисление факториала целого положительного числа — n!.
Пример 6. Найти факториал N!, используя рекурсивную функцию FACT. Вычисление факториала осуществляется по рекуррентной формуле:
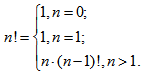
В этой программе рекурсивный процесс с каждым шагом упрощает задачу, сводя n! с помощью рекуррентной формулы к (n-1)! и далее до 1!, который по определению равен единице. Это событие и является решением, обеспечивающим завершение процесса вычисления факториала.
PROGRAM PR6;
VAR N: REAL;
FUNCTION FACT(A: REAL): REAL;
BEGIN
IF (A = 0) OR (A = 1) THEN FACT := 1
ELSE FACT := A * FACT(A - 1) {Рекуррентная формула}
END;
BEGIN
WRITELN(‘Введите число N');
READLN (N);
WRITELN(N: 3:0, '!=', FACT(N): 7:0)
END.
Графическими алгоритмами, в том числе и структурограммой, работу рекурсивной функции объяснить невозможно по той причине, что в оперативной памяти возникает и параллельно существует семейство копий такой функции с разными исходными данными. Пусть мы решаем пример 6 для 5! Временная диаграмма вычислительного процесса представлена на рис. 1.3.
При вводе параметра N = 5 в момент времени Т1, происходит вызов рекурсивной функции FACT(5) из тела основной программы. Вы можете купить Серверы Cisco UCS, которые обладают прекрасной вычислительной платформой по доступной цене. Управление передается функции. В соответствии с рекуррентной формулой в теле рекурсивной функции при вызове функции выполняется оператор FACT := А * FACT(A - 1) для А = 5, то есть вызывается функция FACT(4). Это происходит в момент времени Т2. В оперативной памяти создается еще один образ функции FACT и в качестве входного параметра ей дается значение А = 4. С момента времени Т2 по Т9 функция FACT(5) находится в пассивном состоянии, то есть существует, но не работает. С момента времени Т2 по Т3 выполняются операторы функции FACT(4).

Происходит анализ параметра А, и поскольку А = 4, вызывается функция FACT(3) в момент времени Т3. В оперативной памяти создается еще один образ функции FACT и в качестве входного параметра ей дается значение А = 3. С момента Т3 и до момента Т8 функция FACT(4) становится пассивной, поскольку управление она передала функции FACT(3). Функция FACT(3) вызывает функцию FACT(2), а та в свою очередь функцию FACT( 1). Функция FACT(1) является последней в семействе, то есть она возвращает значение равное 1 в функцию FACT(2) в момент времени T6. В этот момент код функции FACT(l) удаляется из оперативной памяти. Функция FACT(2) становится активной, вычисляет значение равное 2 и в момент времени Т7 передает управление FACT(3). Функция FACT(2) в момент времени Т7 удаляется из памяти. Этот процесс продолжается до момента времени Т10, когда рекурсивная функция завершает свою работу, возвращая вычисленное значение коду основной программы. Опыт изучения рекурсивных функций показывает, что, несмотря на приведенное выше подробное описание, программист все же плохо чувствует работу рекурсивных программ, поскольку принцип их действия выходит за рамки интуитивного понимания процессов программирования.
Предыдущая статья: Использование массивов и функций в качестве формального параметра.
Оглавление: Лекции по Pascal. Часть 2.
Следующая статья: Описание процедур.
Популярные уроки
- Тип данных Boolean. Значения True, False в Pascal.
- Textcolor, Window, Textbackground в Pascal.
- Процедуры Dec и Inc в Pascal.
- Функции trunc, round в Pascal.
- Тип данных Char. Функции Ord, Chr.
- Функции Pred, Succ в Pascal.
- Функции Sqr, Abs, Sqrt, Sin, Cos, Arctan, Ln, Exp, Pi в Pascal.
- Умножение, деление, сложение, вычитание вещественных чисел в Pascal.
- Логические операции с целыми числами.
- Строковые константы в Pascal.