Вычисление предела последовательности.

Вычисление предела последовательности является типичной задачей на использование итерационного цикла.

Последовательность {Xn} определена следующим образом:

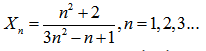
Найти предел последовательности {Xn}, принимая за него такое Хn, при котором |Xn – Xn-1| < ?.

PROGRAM PR24;
VAR      
X, X1, E: REAL;
N: INTEGER;
BEGIN
     WRITELN('BBEДИTE E');
     READLN(E);
     N := 1;
     X := 1;
         REPEAT
            X1 := X;
            X := ( N * N +2)/(3*N * N – N +1);
            N:=N+ 1;
        UNTIL ABS(X – X1) <E;
    WRITELN('Предел последовательности равен', X:12:8)
END.

Вычисление суммы бесконечного ряда с использованием рекуррентной формулы.

Для вычисления на компьютере сумм бесконечного ряда часто используют рекуррентные формулы, с помощью которых друг за другом вычисляют значения членов бесконечной последовательности. Рекуррентные формулы существенно сокращают время работы программы, упрощают процесс написания программы и ее отладки. Как правило, рекуррентные формулы программист должен составить сам. В этом и состоит искусство программирования вычислительных процессов. Рекуррентная формула может и отсутствовать. В этом случае каждый член ряда придется рассчитывать «в лоб» по полной формуле.
Есть определенные признаки, которые помогают выявить наличие рекуррентных формул. К таким признакам относятся выражения (-1)ⁿ, Xⁿ, n! и подобные этим выражения, присутствующие в формуле общего члена бесконечного ряда. Часто рекуррентная формула для бесконечного ряда находится путем деления соседних членов ряда друг на друга.

Пример №25. Вычислить:

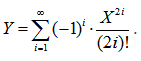
Вычисление ряда окончить при выполнении условия:

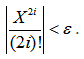Для решения этой задачи необходимо использовать рекуррентную формулу. А найти ее можно следующим способом. Сделаем преобразование исходного ряда в следующий вид:

Тогда условие окончания вычислений будет выглядеть так | Ai | < ?.  Это условие либо выполнится для некоторого i = n и вычислительный процесс будет завершен, либо не выполнится. Во втором случае используют термин «зависание программы». Оператор ЭВМ искусственно останавливает программу и выясняет причину зависания: неправильные исходные данные, например, комбинация X и ?, или допущена ошибка в тексте программы, а может быть получена неправильная рекуррентная формула, или другая причина имеет место. Если Вам понадобятся аксессуары для телефонов, Вы  всегда сможете купить их в интернет-магазине гаджетов http://promate-rus.com/ по оптимальной и доступной цене.
Нас в этом примере интересует нормальный режим работы программы, а это означает, что существует такое n, для которого справедливы следующие формулы:

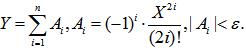
Эти формулы и будут исходными для нашей задачи. На этом первый этап подготовки бесконечного ряда к нахождению его суммы Y с погрешностью ? на компьютере завершается. Если рекуррентную формулу найти невозможно или нет в этом необходимости, то можно ограничиться только приведенными выше преобразованиями.
Но в нашем случае нужен второй этап преобразования, а именно, нахождение рекуррентной формулы. Для этого поделим два соседних члена А_i, А_i-1 (Иногда, с точки зрения математических преобразований проще будет разделить А_i+1 на А_i, что эквивалентно):

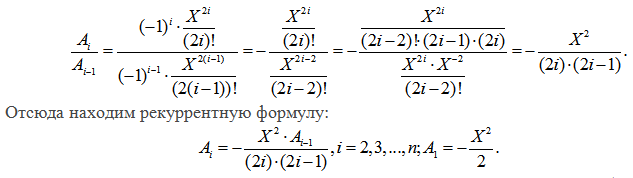
PROGRAM PR25;
VAR      
Y, Е, А, X: REAL;
I: INTEGER;
BEGIN   
     WRITELN('Введите X, E');
     READLN(X, E);
     I:= 1;
     A:= -X*X/2;
   Y:=A;
        WHILE ABS(A) >= E
        DO BEGIN
              I := I+1;
              A:= -X*X/2/I/(2*I - 1)*A;
              Y := Y + A;
       END;
    WRITELN('Y=', Y:10:6)
END.

---

Предыдущая статья: Вложенный арифметический цикл. Часть 2.
Оглавление: Лекции по Pascal.
Следующая статья: Вложенные итерационные циклы.

---