Примеры линейных программ.

В данной статье приводится несколько примеров линейных программ на языке программирования Паскаль.

Пример 3. Рассчитать площадь шара в кв. см. Радиус шара ввести с клавиатуры в миллиметрах.

PROGRAM PR3;        {Программа вычисляет площадь поверхности шара}
VAR PL: REAL;           { PL - площадь шара}
R: INTEGER;               { R - радиус }
BEGIN
WRITELN('Введите радиус шара, мм');
READLN(R);
PL:=4*PI*SQR(R)/100;
WRITELN('Площадь шара =', PL:8:1, 'кв. см')
END.

Пример 4. Осуществить расчеты по формуле:

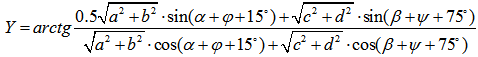
где ?=arctg(b/a), ?=arctg(d/c), c=n*a, d=m*b.
Поскольку набор символов, используемых в идентификаторах переменных в программе (латиница), не включает традиционные для тригонометрии символы греческого алфавита ?, ?, ?, ?, необходимо составить таблицу имен, которая установит соответствие между идентификаторами переменных и этими символами. В таблице имен мы также зафиксируем промежуточные (рабочие) переменные, упрощающие программирование исходной формулы:

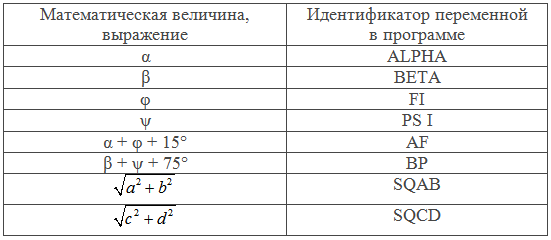
Программирование линейных вычислительных процессов очень похоже на вычисления по формулам, которые математик осуществляет на бумаге. Алгоритм таких вычислений, как правило, не составляется в виде блок-схем. Наиболее удобной формой представления такого алгоритма является формульно-словесный способ, при котором действия пронумерованы пунктами 1, 2, 3 и т.д. Каждое действие поясняется словами, формулами и расчетами.
Алгоритм решения этой задачи описан формульно-словесным способом:

1. Ввод с клавиатуры параметров А, В, М, N, ALPHA, BETA.
2. Вычисление аргументов тригонометрических функций по формулам:

где AF и BP промежуточные рабочие переменные, которые в исходной формуле встречаются по два раза в числителе и знаменателе. Следует отметить, что аргументы встроенных функций Sin и Cos в Паскале должны задаваться в радианах. В исходной формуле подразумевается, что углы ?, ?, ?, ? измеряются в радианах. Поэтому углы 15° и 75° градусов подлежат пересчету в радианы, что и сделано в приведенных выше формулах для расчета AF и BP.
3. Последовательное вычисление величин С, D, FI, PSI по формулам:
C = n*a, D = m*b, FI = arctg(b/a), PSI = arctg(d/c).
4. Нахождение значений промежуточных переменных SQAB и SQCD по формулам:

5. Вычисление Y по упрощенной формуле за счет уже выполненных в предыдущих пунктах алгоритма расчетов.

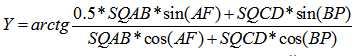6. Последним пунктом этого алгоритма является вывод найденного значения Y на экран монитора.
PROGRAM PR4;
VAR
ALPHA, BETA, FI, PSI, SQAB, SQCD, AF, BP, А, В, C, D, N, M, Y: REAL;
BEGIN
  WRITELN('Введите значения А, В, M, N');
  READLN(A, В, M, N);
  WRITELN('Введите значения АЛЬФА, БЕТТА');
  READLN(ALPHA, BETA);
  С := N*A;
  D := M*B;
  FI := ARCTAN(B/A);
  PSI := ARCTAN(D/C);
  AF := ALPHA + FI + 15*PI/180;
  BP = BETA + PSI + 75*PI/180;
  SQAB := SQRT(A*A + B*B);
  SQCD := SQRT(C*C + D*D);
  Y:=ARCTAN((0.5*SQAB*SIN(AF)+SQCD*SIN(BP))/(SQAB*COS(AF) + SQCD*COS(BP)));
  WRITELN('Y =', Y:7:3)
END.
Следует выделить следующие типичные действия программиста при разработке программ такого класса (формализация линейного вычислительного процесса).
1. Формирование таблицы имен. На этом этапе подбираются латинские обозначения (идентификаторы) для отображения в программе математических величин, используемых в формулах. Для некоторых выражений, встречающихся в формулах два и более раза, можно ввести свои идентификаторы (временные переменные). Эти величины рассчитываются один раз перед основной формулой (формулами), что упрощает исходные формулы и ускоряет расчеты.
2. Учитывая последовательный принцип выполнения операторов в программе – друг за другом по мере их написания – необходимо установить порядок расчета формул. Основное требование состоит в том, чтобы при расчете формулы все переменные и параметры были ранее вычислены или введены с клавиатуры. Если формулы можно упростить путем алгебраических преобразований, то это нужно сделать до начала программирования.
3. Все математические величины нужно разбить на две группы: константы и переменные. Константы следует определить в разделе CONST программы, а переменные — в разделе VAR.
4. Проанализировав возможные значения переменных и требуемую точность расчетов, следует определить тип каждой переменной.
5. Требуется проанализировать все переменные из раздела VAR и определить, какие из них вводятся с клавиатуры, а какие вычисляются по ходу программы.
6. Если в тригонометрических функциях в качестве аргументов используются величины в градусах, то необходимо в программе сделать преобразование этих величин в радианы.
7. При выводе результатов расчетов на экран нужно выбрать формат, способ представления результатов (с плавающей или с фиксированной точкой) и задать точность (число значащих чисел).

Пример 5. Осуществить расчеты по формуле:

Для решения этой задачи следует использовать известные математические преобразова-ния, которые приведут исходную формулу к виду, удобному для программирования. Современный платежный агрегатор net2pay.ru благодаря удобному и интуитивно понятному интерфейсу позволит вести Ваш бизнес в любой точке мира. Эти преобразования описаны в следующей таблице:

PROGRAM PR5;
VAR   
X, Y: REAL;
N: INTEGER;
BEGIN  
   WRITELN('Введите значения X, N');
   READLN(X, N);
   Y := EXP(LN(ABS(EXP((N+1)*LN(X)) + LN(ABS(X+1))/LN(N)))/N);
   WRITELN( Y = ', Y:8:4)
END.

Предыдущая статья: Линейные процессы вычислений.
Оглавление: Лекции по Pascal.
Следующая статья: Разветвляющийся вычислительный процесс.